后缀自动机 | nihility

字符串

发布日期: 2022-07-27

更新日期: 2022-08-27

文章字数: 2.9k

阅读时长: 12 分

后缀自动机，又称为SAM，是个有限状态自动机，我们可以把它看作一张有向拓扑图。由一个起点、若干终点组成。原串的所有子串和从SAM起点开始的所有路径一一对应，不重不漏。所有到达终点的路径就是原串的一个后缀。其中，每个点包含若干子串，每个子串都一一对应一条从起点到该点的路径，这些子串都是最长子串的连续后缀，而连续是什么意思呢，比如说你这个子串是aabbc，则aabbc、abbc、bbc、bc就是连续后缀，可以理解为长度连续的后缀。后缀自动机中包含两种边，一种是普通边，表示在某个状态所表示的所有子串的后面添加一个字符；另一种是Link（fa）边，表示将某个状态所表示的最短子串的首字母删除，这类边构成一棵树。值得一提的是，后缀自动机中点和边的数量都是$O(n)$的，点数$\le 2n$，边数$\le 3n$，且构造的时间复杂度是$O(n)$的

SAM的构造思路

我们定义$endpos(s)$代表子串$s$所有出现位置（尾字母位置）的集合，$SAM$中的每个状态都代表一个$endpos$的等价类。

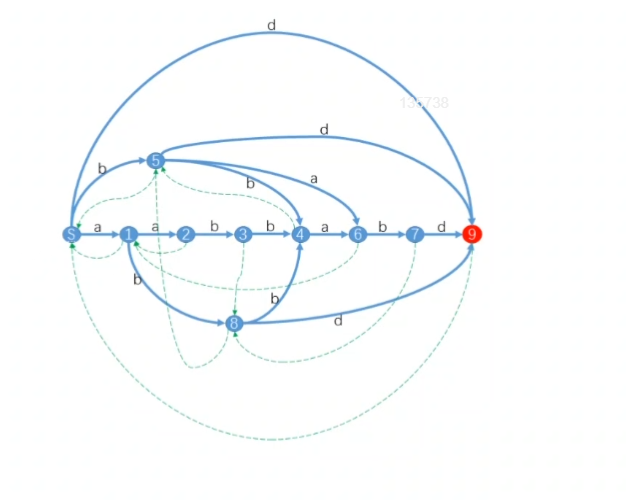
假设$s=aabbabd$，我们易知$E(ab)=(3、6)$，$E$是$endpos$的简写，$E(abb)=E(aabb)=4$，这两个串就属于同一个状态，整个串的后缀自动机如图，蓝色的是普通边，绿色的是Link（fa）边。

$endpos$有很多$useful$的性质

令 $s1、s2$ 为 $S $的两个子串，不妨设 $|s1|≤|s2| $，我们用 $|s| $表示$ s $的长度。则$ s1 $是$ s2$的后缀当且仅当 $endpos(s1)\supseteq endpos(s2) $，$s1$不是$ s2$ 的后缀当且仅当$ endpos(s1)\cap endpos(s2)=\emptyset$
两个不同子串的$endpos$，要么有包含关系，要么没有交集。
两个子串的$endpos$相同，那么短串为长串的后缀。
对于一个状态$ st $，以及任意的$ longest(st) $的后缀$ s $，如果$ s $的长度满足：$|shortest(st)|≤|s|≤|longsest(st)|$，那么$ s∈substrings(st)$

$SAM$也有很好的性质

从起点出发的每一条路径都是原字符串的一个子串，且无重复
不同状态（点）所表示的串一定是没有交集的
一个点和它绿边所指向点的串的长度是连续的
所有绿边构成一棵树
一个状态的$endpos$集合一定包含它入点（通过一条绿边连向它的点）的$endpos$集合，因为该状态只要给串前面加一个字符就能到这些入点状态，特殊地，该状态如果包含原串的前缀串，则$endpos$集合会多一个。而每个状态里最多只有一个前缀。
终点就是包含后缀的点（因为没有出边了）

这些性质都比较容易证明，这里就不赘述了（多用例子代入、并使用反证法）。

那么我们是如何构造出来这个$DFA$的呢？

刚开始我们设起点编号为$1$，它的最大长度为$0$，fa边指向$0$，然后我们从前往后插入每个字符，同时记录$last$为上一次插入后走到的点（初始值为$1$），当插入$1$个字符$c$时，执行如下步骤：

创建一个新状态$np$，并将$len[np]$赋值为$len[last]+1$
从$last$开始跳$fa$边（包括$last$），直到该状态存在到字符$c$的转移停下来，否则就给该状态添加一个到$c$的转移，停下来的状态记为$p$
如果$p$走到了$0$号点，将$fa[np]$赋值为$1$，并退出，否则继续执行
将$p$通过$c$转移到的状态记为$q$，分情况讨论
若$len(p)+1=len(q)$，将$fa[np]$赋值为$q$并退出
否则就新建一个状态$nq$，拷贝$q$的信息，并把$len[nq]$赋值为$len[p]+1$，赋值之后将$fa[q]$和$fa[np]$都赋值为$nq$，并跳$fa$边并把原本通过$c$转移到$q$的改为转移到$nq$

Talk is cheap，show me the code.

代码实现

int tot=1,last=1;//tot是总点数,last是上一个插入的点,空节点编号为1
struct Node{//每个节点
    int len,fa;//len表示该状态的最长子串的长度,fa是它绿边连向的父亲
    int ch[26];
}node[N];//N的大小为二倍的字符串长度,node[1].len=node[1].fa=0,转移数不会超过3倍的字符串长度
char str[N];
int f[N];//f[i]代表i这个状态的endpos的集合大小
void extend(int c){
    int p=last,np=last=++tot;
    f[tot]=1;//tot节点就是该字符串的一个前缀
    node[np].len=node[p].len+1;
    for(;p&&!node[p].ch[c];p=node[p].fa) node[p].ch[c]=np;//从p开始跳fa,并向新点连边直到原本边就存在
    if(!p) node[np].fa=1;//路上所有点都不存在向c的边,那么把新点的fa置为1
    else{
        int q=node[p].ch[c];//否则找到走到的状态
        if(node[q].len==node[p].len+1) node[np].fa=q;//看p与q的len的差值
        else{
            int nq=++tot;//否则新建一个
            node[nq]=node[q],node[nq].len=node[p].len+1;
            node[q].fa=node[np].fa=nq;
            for(;p&&node[p].ch[c]==q;p=node[p].fa) node[p].ch[c]=nq;//把链上的边都指向nq
        }
    }
}
int main(){
    scanf("%s",str);
    for(int i=0;str[i];i++) extend(str[i]-'a');
    return 0;
}

求不同子串的数量

相当于$DAG$上$DP$

ll ans[N];
bool vis[N];
ll dfs(int x){//dfs(1)后ans[1]即为答案
    if(vis[x]) return ans[x];
    vis[x]=1;
    for(int i=0;i<26;i++) if(node[x].ch[i]) ans[x]+=dfs(node[x].ch[i])+1;
    return ans[x];
}

求每种子串出现的次数

每个子串所在状态的$endpos$的集合的大小即为答案

求两个字符串的最长公共子串

scanf("%s",s);
for(int i=0;s[i];i++) extend(s[i]-'a');//首先对一个串建立后缀自动机
//然后让第二个串在后缀自动机上跑
int p=1,t=0,ans=0;//p是第二个串当前所在的状态,t是当前匹配的字符串的长度
scanf("%s",s);
for(int i=0;s[i];i++){
    int c=s[i]-'a';
    while(p>1&&!node[p].ch[c]) p=node[p].fa,t=node[p].len;//若当前节点无法走到下一个状态,则跳到绿边所指位置,因为只有它有可能可以走到以s[i]字母为后缀的位置,类似于kmp的时间复杂度分析,该算法也是线性的
    if(node[p].ch[c]) p=node[p].ch[c],t++;
    else p=1,t=0;
    ans=max(ans,t);
}

求经过每一个点的子串个数

//子串字典序相同但出现位置不同算作多个
//ans[i]就代表着以i能转移到的位置结尾的子串个数
ll ans[N];//初始时ans[i]=f[i](i!=1),ans[1]=f[1]=0
bool vis[N];
ll dfscnt(int u){
	if(vis[u]) return ans[u];
	vis[u]=1;
	for(int i=0;i<26;i++)
		if(node[u].ch[i])
			ans[u]+=dfscnt(node[u].ch[i]);
	return ans[u];
}
//若要求是本质不同子串,初始时ans[i]=f[i]=1(i!=1),ans[1]=f[1]=0即可

求一个字符串的两个前缀的最长公共后缀

当两个前缀不同时，答案就是这两个前缀的状态点在$fa$树上的$lca$

找出所有终止状态

$extend$完之后从$last$跳$fa$即可

找出fa树的bfs序（自动机的拓扑序）

//排完之后就是fail树的bfs序/自动机的拓扑序
for(int i=1;i<=node;i++) cnt[node[i].len]++;
for(int i=1;i<=node;i++) cnt[i]+=cnt[i-1];
for(int i=1;i<=node;i++) q[cnt[node[i].len]--]=i;

公共串

$POI2020$：公共串

这个题和我们求两个串的最长公共子串差不多，我们只需对第一个串建立后缀自动机，然后用后面的串在该后缀自动机上跑，记录后缀自动机每一个状态对应的答案，每个状态的最终答案就是每个字符串（除建立后缀自动机的串）对应该状态答案的最小值，最终答案就是所有状态最终答案的最大值。另外，我们每个串跑完后缀自动机后，我们需要把每个状态的答案传到它的父节点（因为我们在跑后缀自动机的时候可能不会对其父亲状态的答案进行更新，而其父亲是该状态的后缀，肯定需要更新），否则就会出错（例如如下样例）。

#include<bits/stdc++.h>
#define x first 
#define y second
#define endl '\n'
#define lowbit(x) ((x)&(-x))
#define all(x) (x).begin(),(x).end()
#define mp make_pair
#define pb push_back
#define SZ(x) ((int)(x).size())
#define rep(i,a,n) for (int i=a;i<n;i++)
#define per(i,a,n) for (int i=n-1;i>=a;i--)
using namespace std;
typedef pair<int,int> PII;
typedef vector<int> VI;
typedef long long LL;
typedef unsigned long long ULL;
typedef double DB;
mt19937 randint(random_device{}());
mt19937_64 randLL(random_device{}());
template<typename T=int> 
T gcd(T a,T b){return b?gcd(b,a%b):a;}
template<typename T=int> 
T qmi(T a,T b,T p){T res=1;while(b){if(b&1)res=(LL)res*a%p;b>>=1;a=(LL)a*a%p;}return res%p;}
template<typename T=int>
T read(){
	T x=0,f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){
		if(ch=='-')
			f=-1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9'){
		x=x*10+ch-'0';
		ch=getchar();
	}
	return x*f;
}
//----------------------------------------head------------------------------------
const int INF=0x3f3f3f3f,mod=1e9+7,N=4010,M=6010;
const double eps=1e-6;
int tot=1,last=1;//tot是总点数,last是上一个插入的点,空节点编号为1
struct Node{//每个节点
	int len,fa;//len表示该状态的最长子串的长度,fa是它绿边连向的父亲
	int ch[26];
}node[N];//N的大小为二倍的字符串长度,node[1].len=node[1].fa=0,转移数不会超过3倍的字符串长度
char s[N];
int f[N];
int h[N],e[M],ne[M],idx,now[N];
void add(int a,int b){
	e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void extend(int c){
	int p=last,np=last=++tot;
	f[tot]=1;
	node[np].len=node[p].len+1;
	for(;p&&!node[p].ch[c];p=node[p].fa) node[p].ch[c]=np;
	if(!p) node[np].fa=1;
	else{
		int q=node[p].ch[c];
		if(node[q].len==node[p].len+1) node[np].fa=q;
		else{
			int nq=++tot;
			node[nq]=node[q],node[nq].len=node[p].len+1;
			node[q].fa=node[np].fa=nq;
			for(;p&&node[p].ch[c]==q;p=node[p].fa) node[p].ch[c]=nq;
		}
	}
}
void dfs(int u){
	for(int i=h[u];~i;i=ne[i]){
		dfs(e[i]);
		now[u]=max(now[u],now[e[i]]);
	}
}
int ans[N];
void solve(){
	int times=read();
	memset(h,-1,sizeof h);
	scanf("%s",s+1);
	for(int i=1;s[i];i++) extend(s[i]-'a');
	for(int i=1;i<=tot;i++) ans[i]=node[i].len;//保证每个状态的答案不超过其最长子串的大小
	for(int i=2;i<=tot;i++) add(node[i].fa,i);
	while(--times){
		scanf("%s",s+1);
		memset(now,0,sizeof now);//now记录这个子串中各个状态的答案
		int p=1,t=0;
		for(int j=1;s[j];j++){
			int c=s[j]-'a';
			while(p>1&&!node[p].ch[c]) p=node[p].fa,t=node[p].len;
			if(node[p].ch[c]) t++,p=node[p].ch[c];
			else t=0,p=1;
			now[p]=max(now[p],t);
		}
		dfs(1);
		for(int j=1;j<=tot;j++) ans[j]=min(ans[j],now[j]);//取min
	}
	int res=0;
	for(int i=1;i<=tot;i++) res=max(res,ans[i]);//取max
	cout<<res<<endl;
}
signed main(){
	int t=1;
	while(t--) solve();
	return 0;
}